Cross Product
In mathematics and vector calculus, the cross product or vector product (occasionally directed area product to emphasize the geometric significance) is a binary operation on two vectors in three-dimensional space (R3) and is denoted by the symbol ×. Given two linearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with dot product (projection product).
If two vectors have the same direction (or have the exact opposite direction from one another, i.e. are not linearly independent) or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space R3 together with the cross product is an algebra over the real numbers, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.
If two vectors have the same direction (or have the exact opposite direction from one another, i.e. are not linearly independent) or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space R3 together with the cross product is an algebra over the real numbers, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.
Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or "handedness". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.[1] If one adds the further requirement that the product be uniquely defined, then only the 3-dimensional cross product qualifies.
Definition
The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a × b. In physics, sometimes the notation a ∧ b is used,[2] though this is avoided in mathematics to avoid confusion with the exterior product.
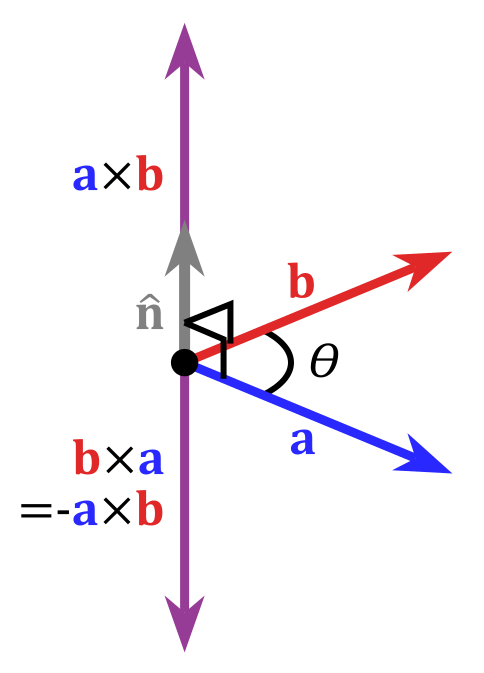
The cross product a × b is defined as a vector c that is perpendicular to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
The cross product a × b is defined as a vector c that is perpendicular to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
The cross product is defined by the formula
where θ is the angle between a and b in the plane containing them (hence, it is between 0° and 180°), ‖a‖ and ‖b‖ are the magnitudes of vectors a and b, and n is a unit vector perpendicular to the plane containing a and b in the direction given by the right-hand rule (illustrated). If the vectors a and b are parallel (i.e., the angle θ between them is either 0° or 180°), by the above formula, the cross product of a and b is the zero vector 0. 

By convention, the direction of the vector n is given by the right-hand rule, where one simply points the forefinger of the right hand in the direction of a and the middle finger in the direction of b. Then, the vector n is coming out of the thumb (see the picture on the right). Using this rule implies that the cross-product is anti-commutative, i.e., b × a = −(a × b). By pointing the forefinger toward b first, and then pointing the middle finger toward a, the thumb will be forced in the opposite direction, reversing the sign of the product vector.
Using the cross product requires the handedness of the coordinate system to be taken into account (as explicit in the definition above). If a left-handed coordinate system is used, the direction of the vector n is given by the left-hand rule and points in the opposite direction.
This, however, creates a problem because transforming from one arbitrary reference system to another (e.g., a mirror image transformation from a right-handed to a left-handed coordinate system), should not change the direction of n. The problem is clarified by realizing that the cross product of two vectors is not a (true) vector, but rather a pseudovector. See cross product and handedness for more detail.
Coordinate notation
The standard basis vectors i, j, and k satisfy the following equalities in a right hand coordinate system:
which imply, by the anticommutativity of the cross product, that
The definition of the cross product also implies that
 (the zero vector).
(the zero vector).
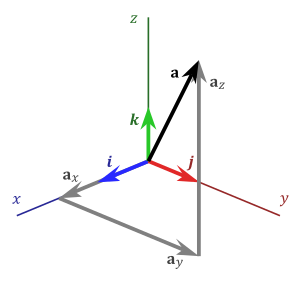
These equalities, together with the distributivity and linearity of the cross product (but both do not follow easily from the definition given above), are sufficient to determine the cross product of any two vectors u and v. Each vector can be defined as the sum of three orthogonal components parallel to the standard basis vectors:
Their cross product u × v can be expanded using distributivity:
This can be interpreted as the decomposition of u × v into the sum of nine simpler cross products involving vectors aligned with i, j, or k. Each one of these nine cross products operates on two vectors that are easy to handle as they are either parallel or orthogonal to each other. From this decomposition, by using the above-mentioned equalities and collecting similar terms, we obtain:
meaning that the three scalar components of the resulting vector s = s1i + s2j + s3k = u × v are
Using column vectors, we can represent the same result as follows:

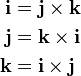
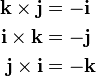

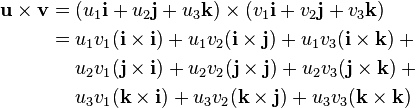
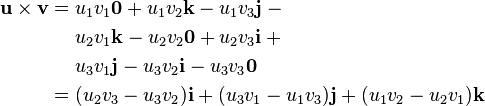
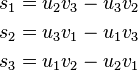

Comments
Post a Comment